📋 Daftar Isi
Pembuktian Proposisi Perihal Himpunan
Proposisi himpunan adalah argumen yang menggunakan notasi himpunan.
Proposisi dapat berupa :
- Kesamaan (identitiy), contoh : Buktikan “A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)”
- Implikasi, contoh : Buktikan bahwa “Jika A ∩ B= ∅ dan A ⊆ (B ∪ C) maka selalu berlaku bahwa A ⊆ C“.
Pembuktian dengan Diagram Venn
Diagram Venn hanya dapat digunakan jika himpunan yang digambarkan tidak banyak jumlahnya. Metode ini lebih mengilustrasikan daripada membuktikan fakta. Diagram Venn tidak dianggap sebagai metode yang valid untuk pembuktian secara formal
Contoh: Misalkan A, B, dan C adalah himpunan. Buktikan bahwa A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) dengan diagram Venn.
Bukti :
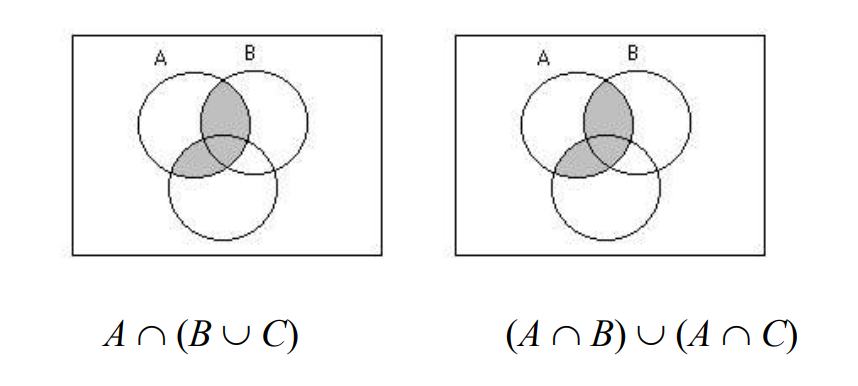
Kedua diagram Venn memberikan area arsiran yang sama. Terbukti bahwa A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
Pembuktian dengan Tabel Keanggotaan
Contoh: Misalkan A, B, dan C adalah himpunan. Buktikan bahwa A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
| A | B | C | B ∪ C | A ∩ (B ∪ C) | A ∩ B | A ∩ C | (A ∩ B) ∪ (A ∩ C) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Pembuktian dengan Aljabar Himpunan
Contoh 1: Misalkan A dan B himpunan. Buktikan bahwa (A ∩ B) ∪ (A ∩ Bc) = A
Bukti:
(A ∩ B) ∪ (A ∩ Bc) = A ∩ (B ∪ Bc) (Hukum Distributif)
(A ∩ B) ∪ (A ∩ Bc) = A ∩ U (Hukum Komplemen)
(A ∩ B) ∪ (A ∩ Bc) = A (Hukum Identitas)
Contoh 2: Misalkan A dan B himpunan. Buktikan bahwa A ∪ (B – A) = A ∪ B
Bukti:
A ∪ (B – A) = A ∪ (B ∩ Ac) (Definisi Operasi Selisih)
A ∪ (B – A) = (A ∪ B) ∩ (A ∪ Ac) (Hukum Distributif)
A ∪ (B – A) = (A ∪ B) ∩ U (Hukum Komplemen)
A ∪ (B – A) = A ∪ B (Hukum Identitas)
Pembuktian dengan Definisi
Metode ini digunakan untuk membuktikan pernyataan himpunan yang tidak berbentuk kesamaan, tetapi pernyataan yang berbentuk implikasi. Biasanya di dalam implikasi tersebut terdapat notasi himpunan bagian (⊆ atau ⊂).
Contoh: Misalkan A dan B himpunan. Jika A ∩ B = ∅ dan A ⊆ (B ∪ C) maka A ⊆ C. Buktikan!
Bukti:
- Dari definisi himpunan bagian, P ⊆ Q jika dan hanya jika setiap x ∈ P juga ∈ Q. Misalkan x ∈ A. Karena A ⊆ (B ∪ C), maka dari definisi himpunan bagian, x juga ∈ (B ∪ C). Dari definisi operasi gabungan (∪), x ∈ (B ∪ C) berarti x ∈ B atau x ∈ C
- Karena x ∈ A dan A ∩ B = ∅, maka x ∉ B
Dari pembuktian di atas, x ∈ C harus benar. Karena ∀x ∈ A juga berlaku x ∈ C, maka dapat disimpulkan A ⊆ C.
Materi Lengkap
Silakan baca juga beberapa artikel menarik kami tentang Matematika Diskrit – Himpunan, daftar lengkapnya adalah sebagai berikut.




