📋 Daftar Isi
Lintasan dan Sirkuit Euler
Lintasan Euler ialah lintasan yang melalui masing-masing sisi di dalam graf tepat satu kali.
Sirkuit Euler ialah sirkuit yang melewati masing-masing sisi tepat satu kali.
Graf yang mempunyai sirkuit Euler disebut graf Euler (Eulerian graph). Graf yang mempunyai lintasan Euler dinamakan juga graf semi-Euler (semi-Eulerian graph).
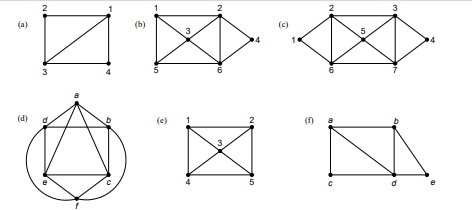
Lintasan Euler pada graf (a) : 3, 1, 2, 3, 4, 1
Lintasan Euler pada graf (b) : 1, 2, 4, 6, 2, 3, 6, 5, 1, 3
Sirkuit Euler pada graf (c) : 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1
Sirkuit Euler pada graf (d) : a, c, f, e, c, b, d, e, a, d, f, b, a
Graf (e) tidak mempunyai lintasan maupun sirkuit Euler
Graf (f) mempunyai lintasan Euler: a, c, d, a, b, e, d, b
Keterangan:
(a), (b), dan (f) graf semi-Euler
(c) dan (d) graf Euler
(e) bukan graf semi-Euler maupun graf Euler
Teorema 1
Graf tidak berarah memiliki lintasan Euler (graf semi-Euler) jika dan hanya jika terhubung dan memiliki dua buah simpul berderajat ganjil atau tidak ada simpul berderajat ganjil sama sekali.
Teorema 2
Graf tidak berarah G adalah graf Euler (memiliki sirkuit Euler) jika dan hanya jika setiap simpul berderajat genap.
Teorema 3
- Graf berarah G memiliki sirkuit Euler jika dan hanya jika G terhubung dan setiap simpul memiliki derajat-masuk dan derajat-keluar sama.
- G memiliki lintasan Euler jika dan hanya jika G terhubung dan setiap simpul memiliki derajat-masuk dan derajat-keluar sama kecuali dua simpul, yang pertama memiliki derajat-keluar satu lebih besar derajat-masuk dan yang kedua memiliki derajat-masuk satu lebih besar dari derajat-keluar.
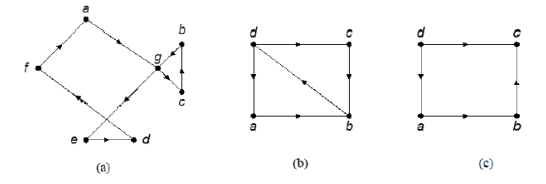
Keterangan:
(a) Graf berarah Euler (a, g, c, b, g, e, d, f, a)
(b) Graf berarah semi-Euler (d, a, b, d, c, b)
(c) Graf berarah bukan Euler maupun semi-Euler
sumber: Matematika Diskrit (Rinaldi Munir)
Materi Lengkap
Silakan baca juga beberapa artikel menarik kami tentang Graf, daftar lengkapnya adalah sebagai berikut.



