📋 Daftar Isi
Menambahkan Simpul Baru
Pertama kita akan memodifikasi structure yang digunakan untuk membuat simpul-simpul pada tree. Pada AVL Tree, kita memerlukan informasi height atau tinggi pohon untuk memeriksa keseimbangan pohon. Pada struct node, kita tambahkan satu elemen tambahan:
int height;
Saat kita ingin membuat sebuah simpul baru, kita menggunakan fungsi struct node *newNode(int data). Pada fungsi tersebut, kita tambahkan satu baris program untuk menginisialisasi nilai height.
new_node->height = 1;
Simpul baru pada awalnya ditambahkan sebagai daun, oleh karena itu heightnya bernilai 1.
Kemudian, kita modifikasi fungsi insert. Perbedaan AVL Tree dibandingkan dengan BST adalah AVL Tree selalu memastikan keseimbangan pohon setiap kali ada simpul baru yang ditambahkan atau dihapus dari pohon (self balancing binary search tree). Tahapan untuk menambahkan simpul baru pada AVL Tree adalah sebagai berikut:
- Lakukan insert seperti halnya pada BST
- Perbarui height untuk seluruh node, mulai dari node yang terakhir ditambahkan hingga ke root. Height node adalah height subtree kiri atau subtree kanan yang ada di bawahnya ditambahkan dengan 1.
- Hitung balance factor untuk seluruh node, mulai dari node yang terakhir ditambahkan hingga ke root, untuk menentukan apakah node balanced atau tidak
- Jika node unbalanced, lakukan rotasi. Ada 4 kasus rotasi, bergantung kepada posisi node terbawah.
- Hasil akhir fungsi adalah mengembalikan node yang telah balanced.
Jika kita perhatikan, tahapan-tahapan di atas dilakukan secara berulang-ulang untuk node-node yang ada pada tree. Oleh karena itu, tahapan tersebut akan diimplementasikan secara rekursif. Jika diimplementasikan, kelima tahapan di atas dapat dituliskan seperti berikut ini.
struct node* insert(struct node* root, int newData)
{
//1. Lakukan BST insert biasa
if(root == NULL)
{
return(newNode(newData));
}
//asumsi tidak boleh ada nilai yang sama dalam BST
if (newData < root->data)
root->left = insert(root->left, newData);
else if (newData > root->data)
root->right = insert(root->right, newData);
//2. Update height dari node baru sampai root
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
//3. Hitung balance faktor untuk menentukan apakah node balance atau unbalanced
int balance = getBalanceFactor(root);
//Jika tidak balance return hasil rotation
//Kasus 1: Left Left
if (balance > 1 && newData < root->left->data)
return rightRotate(root);
//Kasus 2: Right Right
if (balance < -1 && newData > root->right->data)
return leftRotate(root);
//Kasus 3: Right Left
if (balance < -1 && newData < root->right->data)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
//Kasus 4: Left Right
if (balance > 1 && newData > root->left->data)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
//Rreturn node jika balance
return root;
}
Ganti fungsi insert yang sudah ada di Praktikum9A.c dengan fungsi insert di atas. Perhatikan bahwa pada fungsi insert di atas terdapat beberapa fungsi tambahan yang dipanggil untuk membantu proses insert simpul baru ke dalam AVL Tree, antara lain:
- max, fungsi untuk mencari tinggi maksimum antara node kiri dan node kanan
- getHeight, fungsi untuk mencari tinggi sebuah node
- getBalanceFactor, fungsi untuk menghitung balance faktor sebuah node
- rightRotate, fungsi untuk rotasi kanan
- leftRotate, fungsi untuk rotasi kiri
int max(int a, int b)
{
if (a > b) return a;
else return b;
}
int getHeight(struct node* N)
{
if (N == NULL)
return 0;
return N->height;
}
//Hitung balance factor untuk node N
int getBalanceFactor(struct node*N)
{
if (N == NULL)
return 0;
return getHeight(N->left) - getHeight(N->right);
}
struct node* rightRotate(struct node *T)
{
struct node *newRoot = T->left;
struct node *orphan = newRoot->right;
//Lakkukan Rotasi
newRoot->right = T;
T->left = orphan;
//Update Height
T->height = max(getHeight(T->left), getHeight(T->right))+1;
newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right))+1;
//Return root baru
return newRoot;
};
struct node *leftRotate(struct node* T)
{
struct node *newRoot = T->right;
struct node *orphan = newRoot->left;
//Lakukan rotasi
newRoot->left = T;
T->right = orphan;
//Update height
T->height = max(getHeight(T->left), getHeight(T->right))+1;
newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right))+1;
//Return root baru
return newRoot;
};
Untuk menguji apakah fungsi insert tersebut bisa dijalankan, cobalah untuk menginisiasi tree dan menambahkan beberapa simpul, lalu menampilkannya secara preorder, inorder, atau postorder. Contoh:
struct Node *root = NULL;
root = insert(root, 9);
root = insert(root, 5);
root = insert(root, 10);
root = insert(root, 0);
root = insert(root, 6);
root = insert(root, 11);
root = insert(root, -1);
root = insert(root, 1);
root = insert(root, 2);
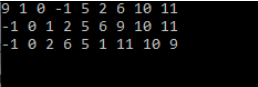
Jika berhasil, maka akan muncul tampilan seperti ini di layar:
Menghapus Sebuah Simpul
Tahapan pada penghapusan simpul AVL Tree mirip dengan tahapan penambahan simpul baru yang telah dijelaskan di atas. Penghapusan simpul pada AVL Tree dilakukan dengan cara yang sama seperti penghapusan simpul pada BST. Namun, setelahnya kita harus mengecek kembali tinggi dan balance
factor untuk setiap node agar keseimbangan pohon tetap terjaga. Tahapan penghapusan simpul pada AVL Tree adalah sebagai berikut:
- Lakukan delete seperti halnya pada BST
- Perbarui height untuk seluruh node, mulai dari node yang terakhir ditambahkan hingga ke root. Height node adalah height subtree kiri atau subtree kanan yang ada di bawahnya ditambahkan dengan 1.
- Hitung balance factor untuk seluruh node, mulai dari node yang terakhir ditambahkan hingga ke root, untuk menentukan apakah node balanced atau tidak
- Jika node unbalanced, lakukan rotasi. Ada 4 kasus rotasi, bergantung kepada posisi node terbawah.
- Hasil akhir fungsi adalah mengembalikan node yang telah balanced.
struct node *delete_node(struct node *root, int deletedData)
{
if(root == NULL)
return;
struct node *cursor;
if(deletedData > root->data)
root->right = delete_node(root->right, deletedData);
else if(deletedData < root->data)
root->left = delete_node(root->left, deletedData);
else
{
//1 CHILD
if(root->left == NULL)
{
cursor = root->right;
free(root);
root = cursor;
}
else if(root->right == NULL)
{
cursor = root->left;
free(root);
root = cursor;
}
//2 CHILD NODE
else
{
cursor = root->right;
while(cursor->left != NULL)
{
cursor = cursor->left;
}
root->data = cursor->data;
root->right = delete_node(root->right, cursor->data);
}
}
//Jika setelah dilakukan delete, tree kosong maka return root
if (root == NULL)
return root;
//2. Update height dari node
root->height = 1 + max(getHeight(root->left), getHeight(root->right));
//3. Hitung balance factor untuk menentukan apakah root balance atau unbalanced
int balance = getBalanceFactor(root);
//Jika tidak balance, return hasil rotation
//Kasus 1: Left Left
if (balance > 1 && getBalanceFactor(root->left) >= 0)
return rightRotate(root);
//Kasus 2: Right Right
if (balance < -1 && getBalanceFactor(root->right) <= 0)
return leftRotate(root);
//Kasus 3: Right Left
if (balance < -1 && getBalanceFactor(root->right) > 0)
{
root->right = rightRotate(root->right);
return leftRotate(root);
}
//Kasus 4: Left Right
if (balance > 1 && getBalanceFactor(root->left) < 0)
{
root->left = leftRotate(root->left);
return rightRotate(root);
}
return root;
};
Untuk memastikan fungsi delete_node tersebut sudah berjalan, cobalah untuk
menghapus salah satu node pada tree, lalu tampilkan kembali isi tree secara preorder, inorder, atau postorder. Contoh:
root=delete_node(root, 10);
Materi Lengkap
Silakan baca juga beberapa artikel menarik kami tentang Tree (Bagian 2), daftar lengkapnya adalah sebagai berikut.




