📋 Daftar Isi
Ilustrasi Topological Order/Sort
Sebelum lebih jauh mengenal topological order, yuk perhatikan ilustrasi berikut.
Untuk mengambil mata kuliah tertentu harus sudah lulus mata kuliah – mata kuliah lain.
Bagaimana seharusnya urutan mata kuliah diambil?

Bagaimana pengurutan pengerjaan jika:
- A harus dikerjakan setelah D dikerjakan
- C baru dapat dikerjakan jika A dikerjakanB dikerjakan jika A dikerjakan
- E dikerjakan jika D dan B selesai dikerjakan
- F dikerjakan jika A dan C selesai dikerjakan
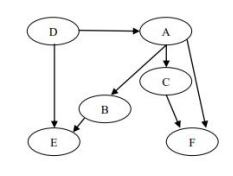
Masalah tersebut dapat diselesaikan dengan topological sort. Selain itu graph harusnya berjenis DAG (Directed Acyclic Graf) = graph berarah dan tidak sirkuler (cycle).
Untuk graph berarah G = (V, E), topological order akan melakukan pengurutan linear node-nodenya sehingga: untuk setiap edge (v, w) di E, v mendahului w dalam urutan

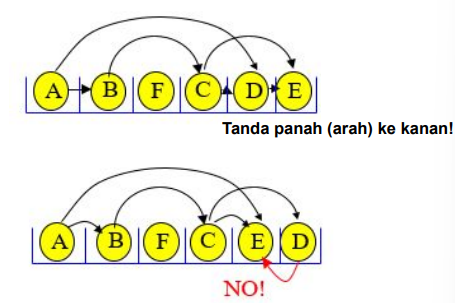
Topological Order/Sort Tidak Unique
Topological sort/order akan memiliki banyak kombinasi dari node yang ada.

- s1 = {a, b, c, d, e, f, g, h, i}
- s2 = {a, c, b, f, e, d, h, g, i}
- s3 = {a, b, d, c, e, g, f, h, i}
- s4 = {a, c, f, b, e, h, d, g, i}
- dan seterusnya
Algoritma Topologi Sort
Langkah 1
Identifikasi node-node yang tidak mempunyai edge yang masuk 🡪 indegree(node)= 0

Jika tidak ada node tersebut berarti cycle 🡪 STOP

Langkah 2
Hapus node tersebut (node dengan indegree 0) dan semua edge yang keluar dari node
tersebut. Tempatkan node tersebut sebagai output.
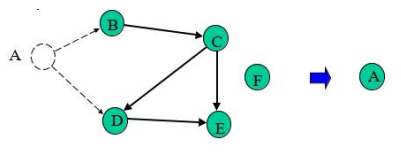
Ulangi langkah 1 dan langkah 2 sampai graph kosong


Materi Lengkap
Silakan baca juga beberapa artikel menarik kami tentang Graph, daftar lengkapnya adalah sebagai berikut.




