📋 Daftar Isi
Matriks Ketetanggaan (Adjacency Matrix)
Misalkan G adalah graf tak berarah dengan titik-titik v1, v2,…,vn (n berhingga).
Matriks ketetanggaan yang sesuai dengan graf G adalah matriks A = (aij) dengan aij = jumlah garis yang menghubungkan titik vi dengan vj
A = [aij],
1, jika simpul i dan j bertetangga(/∑grs)
aij = {
0, jika simpul i dan j tidak bertetangga
Graf direpresentasikan dengan cara menyatakannya dalam jumlah garis yang menghubungkan titik-titiknya. Jumlah baris (dan kolom) matriks ketetanggaan sama dengan jumlah titik dalam graf.
Contoh :
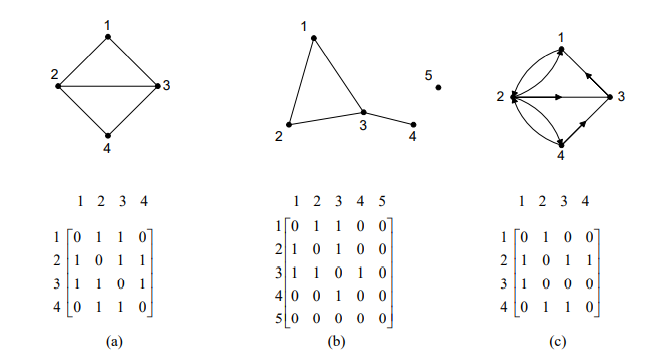
Matriks ketetanggaan nol-satu tidak dapat digunakan untuk merepresentasikan graf yang mempunyai sisi ganda.
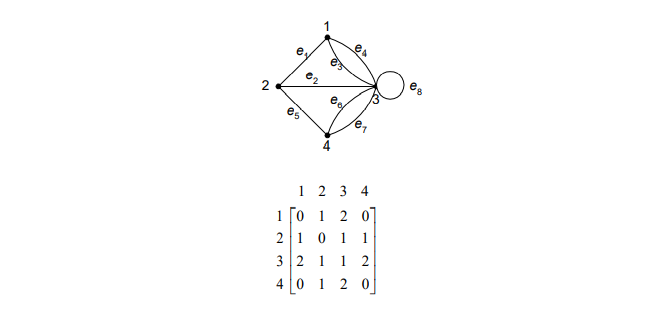
Beberapa hal yang menjadi catatan dalam merepresentasikan graf dalam matrik ketetanggaan:
Matriks ketetanggan untuk graf sederhana dan tidak berarah merupakan matriks simetris.
Graf tidak mempunyai loop jika dan hanya jika semua elemen diagonal utamanya = 0. Loop pada vi bersesuaian dengan aii = 1
Matriks ketetanggaan dapat dipakai untuk mendeteksi graf yang tidak terhubung secara mudah.
Derajat tiap simpul i:
- Untuk graf tak-berarah
- Untuk graf berarah
- Derajat graf G = jumlah semua komponen matriks
Graf G adalah graf Bipartite (Km,n) jika dan hanya jika matriks ketetanggaannya berbentuk
dengan O= matriks 0
1m = matriks m x n semua elemen = 1
1n = matriks n x m semua elemen = 1
G graf lengkap jika dan hanya jika semua elemen dalam diagonal utama = 0, semua elemen di luar diagonal utama = 1.
Matriks ketetanggaan untuk graf berbobot
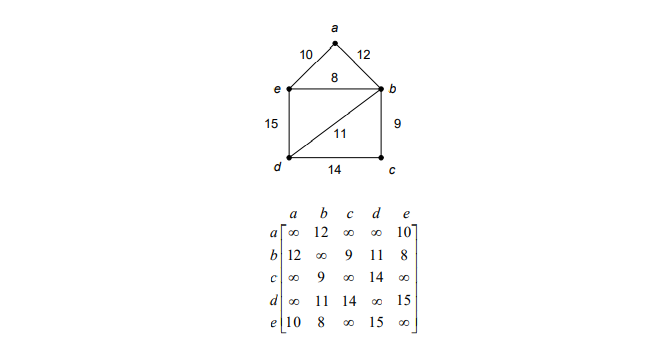
Matriks ketetanggaan dapat dipakai untuk menghitung banyaknya kemungkinan walk dengan panjang tertentu antara 2 titik.
Misalkan A = (aij) matriks ketetanggaan graf G.
An = A×A×A …×A (sebanyak n kali). Banyaknya kemungkinan path dengan panjang n dari titik vi ke vj adalah elemen aij pada matriks An (=aijn)
Matriks Biner (Incidency Matrix)
Misalkan G adalah graf tanpa loop dengan n titik v1, v2, …,vn dan k garis e1, e2, … ek.
Matriks yang sesuai adalah matriks berukuran n × k yang elemennya adalah:
A = [aij],
1, jika simpul i bersisian dengan sisi j
aij = {
0, jika simpul i tidak bersisian dengan sisi j
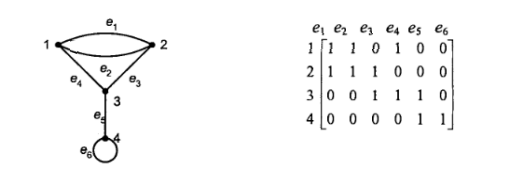
Derajat titik vi = jumlah semua elemen pada baris ke-i
Derajat total = jumlah semua elemen dari matriks
Matriks biner dapat dipakai untuk menyatakan graf secara tepat. Setiap garis berhubungan dengan 2 titik. Maka dalam matriks biner, setiap kolom mempunyai tepat 2 elemen 1, sisanya elemen 0.
Jumlah elemen pada baris ke-i= derajat titik vi. Derajat total graf G= jumlah semua elemen matriks.
Jika semua elemen pada beris ke-i = 0, maka titik vi adalah titik terasing. Dua kolom yang semua elemennya sama menyatakan garis yang parallel atau sisi ganda.
Senarai Ketetanggaan (Adjacency List)
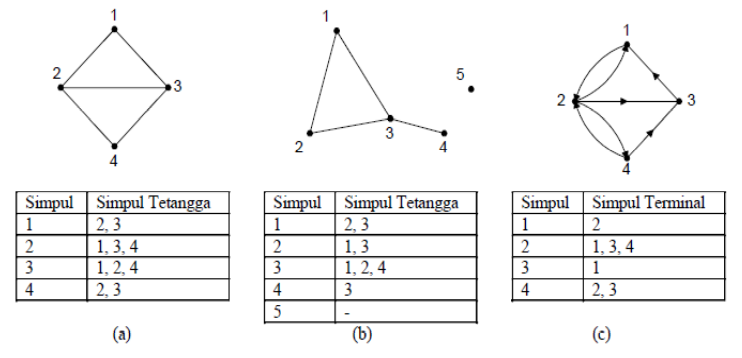
Matriks Sirkuit
Misalkan G graf yang memuat q buah sirkuit sederhana dan e buah garis.
Matriks sirkuit A = (aij) yang bersesuaian adalah matriks yang terdiri dari q baris dan e kolom dengan elemen sebagai berikut:
A = [aij],
1, jika sirkuit ke- i memuat garis ke- j
aij = {
0, jika sirkuit ke- i tidak memuat garis ke- j
Materi Lengkap
Silakan baca juga beberapa artikel menarik kami tentang Graf, daftar lengkapnya adalah sebagai berikut.




